3-April-2017: Centripetal Force with a Motor

Lab#9: Centripetal Force with a Motor
May Soe Moe
Lab Partners: Ben Chen, Steven Castro
3-April-2017

Objective: To come up with a model that describes the relationship between the angular speed ω and the angle θ that was created with the string attaching the rubber stopper while revolving around the y-axis--the surveying tripod. 

Introduction: After getting the apparatus set up first, we tried spinning the rubber stopper attached to a string with motor. We found that the rubber stopper revolved around the y-axis--the central pole or surveying tripod got larger radius and larger angle θ as the motor spin at a higher angular speed ω. We wanted to know the relationship between the angular speed ω and the angle θ. We would draw up free body diagrams of all forces acting on the rubber stopper during revolution and derive the angular speed ω in terms of angle θ. From our setup, we did not know the angle that was forming during the revolution and the way we came up with to measure the angle was by setting a ring stand with honrizontal piece of paper sticking out. Then we adjusted the ring stand's height so that the rubber stopper will hit the horizontal paper. When we got that height, then we could mathematically calculate the angle with all our other measurements and datas. From our setup, we could calculate the missing values such as the angle θ, the radius created by the string with rubber stopper, the total radius (the original radius of the apparatus and the radius created by the string with rubber stopper) using trigonometry. We would calculate our derived angular speed ω equation using the calculated missing values (θ, total radius). We could then compare the values we got from our derived equation and the angular speed formula which we knew-- ω= 2π/T. 

Experimental Procedure:

(1) The apparatus set up was done by the professor as in the picture below:

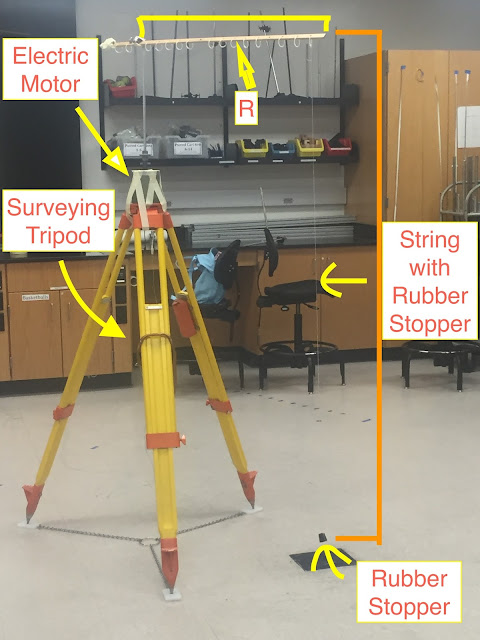Apparatus

Diagram we used for calculating θ, Lsinθ, and Total Radius

(2) The apparatus was set up by putting an electric motor on a surveying tripod, a vertical rod on the motor, a horizontal rod perpendicularly mounted on a vertical rod, a long string tied to the end of the horizontal rod, a rubber stopper at the end of the string, and a ring stand with a horizontal piece of paper sticking out.

(3) We ran the electric motor and let the rubber stopper revolve around the surveying tripod at unknown angular speed ω and angle θ.

(4) We ran the motor at certain angular speed ω and timed the time to complete ten revolutions. And we divided that time by 10 to get the time for one revolution.

(5) We adjusted the ring stand with a horizontal piece of paper sticking out while the rubber stopper was spinning around the tripod to a height when the spinning rubber stopper hit the horizontal paper.

(6) We stopped running the electric motor when the rubber stopper hit the horizontal paper taped to the ring stand. We measured the height of the ring stand from the ground to the horizontal paper.

(7) We also got other measurements such as the Length of R, the length of L, and the length of H as described in the diagram above.

(8) We increased the voltage of the motor driving the system and repeated the same steps for five more times to get our datas.

Calculations:

Calculated Values

Here are the equations that were used to find the values above and some clarifications that might be needed for the column headers.

Here is our free diagram of forces acting on the rubber stopper and our derived equation that represents the relationship between the angle θ and the angular speed ω.

Conclusion: 

We compared the two angular speed ω values we got--values we got from our known angular speed ω equation-- ω= 2π/T, and our derived equation. It turned out that our theoretical values are larger than our experimental values. Our percentage of errors came out to be less than 5% except the last ω. Except our error percentage, our results are in the acceptable range. The last angular speed ω for both using T and using h are very high, thus leading to higher percentage error. Uncertainties or things that led us to commit some errors could be that we assumed the angular speed ω of the string with the rubber stopper was constant throughout the rotation when it could be speeding up over time. We ignored air resistance. The height of the ring stand with horizontal paper sticking out, and the L sin θ values could be smaller than what we recorded in reality, since the rubber stopper hit the horizontal paper when what we should record was the rim of the paper. We took longer time as we had to time the time to complete ten rotations and to adjust the height of the horizontal paper sticking out so that the rubber stopper would hit the paper. During that time of ten revolutions and adjusting the height of the paper, the rubber stopper could be speeding up. Regardless of all the uncertainties and errors, our experimental values came out to be acceptable.