Lab#3: Non-Constant Acceleration Problem
May Soe Moe
Lab Partners: Ben Chen, Steven Castro
Date Performed: 6-March-2017
Objective: To find out the distance of the elephant before coming to rest by numerically and analytically and compare the results
May Soe Moe
Lab Partners: Ben Chen, Steven Castro
Date Performed: 6-March-2017
Objective: To find out the distance of the elephant before coming to rest by numerically and analytically and compare the results
 |
| Problem with Given Information |
Theory/Introduction: We were given the problem, where we wanted to find out how far the elephant goes before coming to rest, meaning we want to find the distance x when the final velocity v is zero. We knew the following information: the mass of the elephant on frictionless roller skates (5000-kg), the velocity of the elephant (25 m/s), the mass of the rocket on the elephant's back (1500-kg), the rocket's thrust (8000N), and the function m(t)= 1500kg-(20kg/s)*t. In order to figure out the distance, we will approach this problem analytically and numerically. For analytical approach, the professor already did a bunch of calculus, integrating, to find the velocity and position function from Newton's Second Law, Fnet=m(t)a. To numerically approach, we used Microsoft Excel to put in the known values and find what we do not know to figure out the distance that we are looking for. We tried to figure it out by letting the Excel calculate the data and see when the velocity is zero from the spreadsheet. Then we compared what we got analytically and numerically.
Summary:
(1) We put in the known values from the given problem into Microsoft Excel: M0=6500 kg, v0= 25m/s, b(burning fuel rate)=20kg/s, Fnet= -8000N. We will set Delta t to be 1 second at first and calculate the acceleration, change in velocity, velocity, change in position, and position at each time interval.
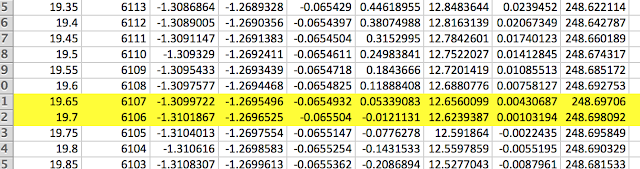
(2) What we wanted to find out was the distance the elephant traveled when its final velocity is zero. Since we don't know when the elephant is at rest, we tried to figure out the time when the velocity is zero by filling down the row.
Summary:
(1) We put in the known values from the given problem into Microsoft Excel: M0=6500 kg, v0= 25m/s, b(burning fuel rate)=20kg/s, Fnet= -8000N. We will set Delta t to be 1 second at first and calculate the acceleration, change in velocity, velocity, change in position, and position at each time interval.
(2) What we wanted to find out was the distance the elephant traveled when its final velocity is zero. Since we don't know when the elephant is at rest, we tried to figure out the time when the velocity is zero by filling down the row.
(3) The concept behind is that we wanted to find out the time it took for the elephant to come to rest because we were using trapezoidal rule to approximate the distance. By making the time interval smaller, the trapezoid gets smaller and it makes accurate approximation of the distance.
 |
| How we got the equation for Change in Velocity. |











No comments:
Post a Comment